import numpy
import matplotlib.pyplot as plt
mean = 0
std = 1
num_samples = 100
samples = numpy.random.normal(mean, std, size=num_samples)
plt.plot(samples)
plt.show()
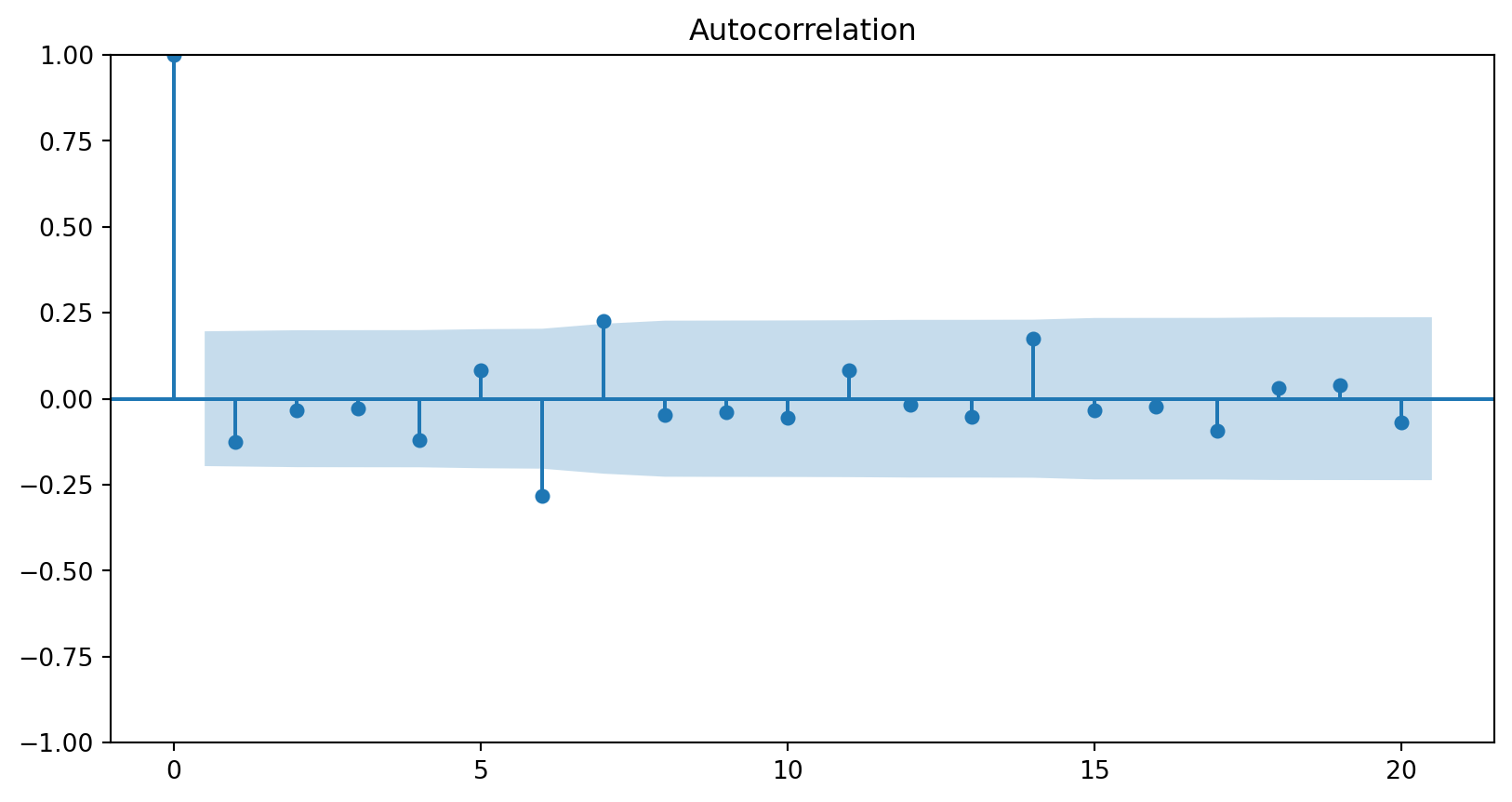
White noise implies stationarity. Stationarity does not imply white noise.
1. Deterministic trend
Yt=f(t)+ϵt
where ϵt∼iid(0,σ2), t=1,2,...T
Mean of the process is time dependent, but the variance of the process is constant.
A trend is deterministic if it is a nonrandom function of time.
2. Random walk
Yt=Yt−1+ϵt
Random walk has a stochastic trend.
Model behind naive method.
A trend is said to be stochastic if it is a random function of time.
3. Random walk with drift
Yt=α+Yt−1+ϵt
Random walk with drift has a stochastic trend and a deterministic trend.
Model behind drift method.
Yt=Yt−1+ϵtY1=Y0+ϵ1Y2=Y1+ϵ2=Y0+ϵ1+ϵ2Y3=Y2+ϵ3=Y0+ϵ1+ϵ2+ϵ3.Yt=Yt−1+ϵt=Y0+ϵ1+ϵ2+ϵ3+...+ϵt=Y0+t∑i=1ϵt
Mean: E(Yt)=Y0.
Variance: Var(Yt)=tσ2.
Yt=Yt−1+ϵtY1=α+Y0+ϵ1Y2=α+Y1+ϵ2=2α+Y0+ϵ1+ϵ2Y3=α+Y2+ϵ3=3α+Y0+ϵ1+ϵ2+ϵ3.Yt=α+Yt−1+ϵt=tα+Y0+ϵ1+ϵ2+ϵ3+...+ϵtYt=tα+Y0+t∑i=1ϵt
It has a deterministic trend (Y0+tα) and a stochastic trend ∑ti=1ϵt.
Mean: E(Yt)=Y0+tα
Variance: Var(Yt)=tσ2.
There is a trend in both mean and variance.
Deterministic trend: Time-trend regression
The trend can be removed by fitting a deterministic polynomial time trend. The residual series after removing the trend will give us the de-trended series.
Stochastic trend: Differencing
The process is also known as a Difference-stationary process.
Integrated to order d: Series can be made stationary by differencing d times.
Question: Show that random walk process is an I(1) process.
The random walk process is called a unit root process. (If one of the roots turns out to be one, then the process is called unit root process.)
| Values | Lag 1 | Lag 2 | |
|---|---|---|---|
| 0 | 1.203587 | NaN | NaN |
| 1 | 1.290288 | 0.086700 | NaN |
| 2 | 0.334784 | -0.955504 | -1.042204 |
| 3 | -0.036386 | -0.371170 | 0.584334 |
| 4 | -1.152387 | -1.116001 | -0.744831 |
| ... | ... | ... | ... |
| 95 | 10.696335 | -0.277457 | -0.910943 |
| 96 | 11.466986 | 0.770650 | 1.048107 |
| 97 | 11.923566 | 0.456580 | -0.314070 |
| 98 | 11.149137 | -0.774429 | -1.231009 |
| 99 | 11.190200 | 0.041062 | 0.815491 |
100 rows × 3 columns
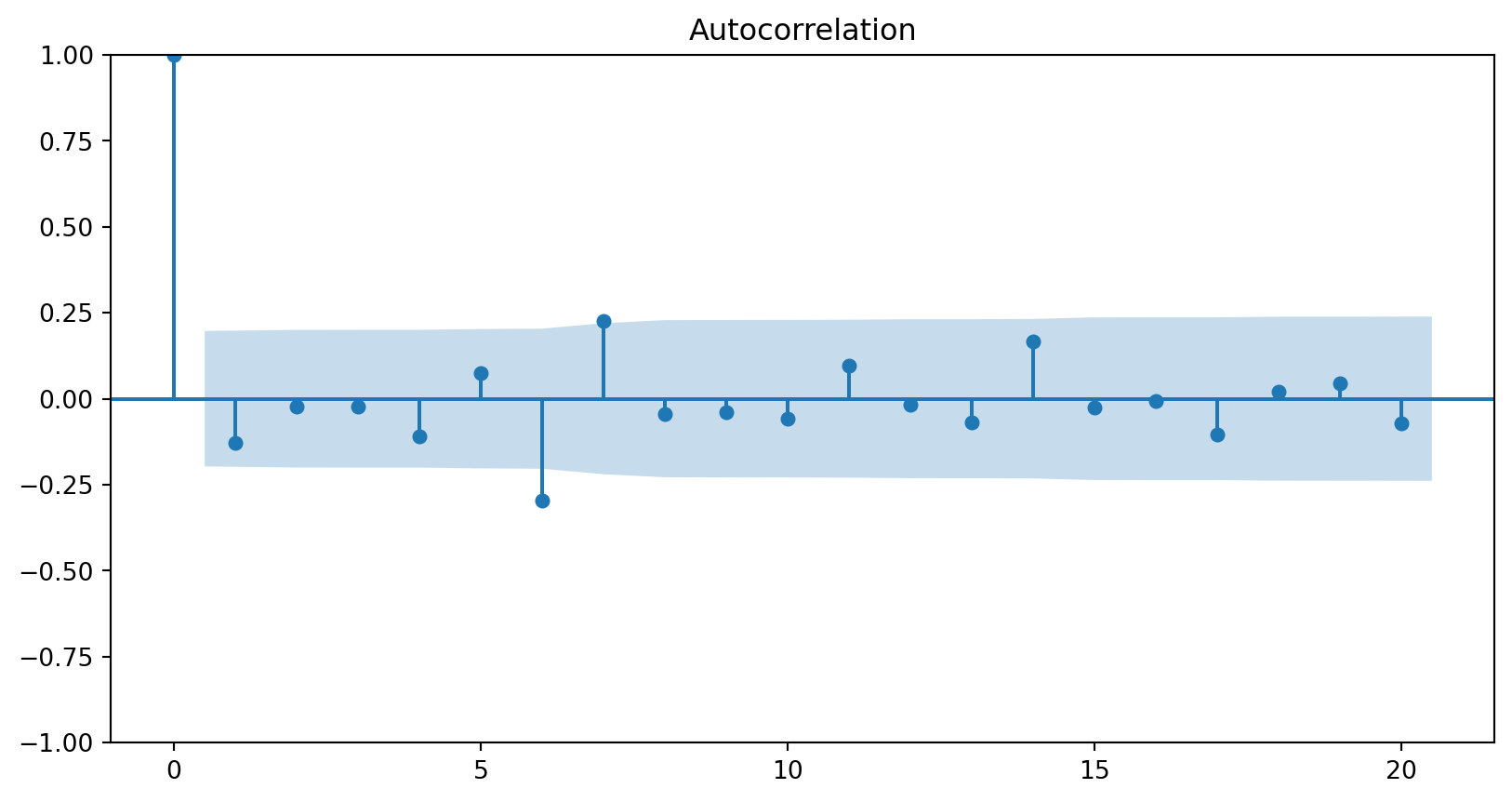
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(9,7), 'figure.dpi':120})
# Import data
df = pd.read_csv('wwwusage.csv', names=['value'], header=0)
# Original Series
fig, axes = plt.subplots(2, 2, sharex=True)
axes[0, 0].plot(df.value); axes[0, 0].set_title('Original Series')
plot_acf(df.value, ax=axes[0, 1], lags=np.arange(len(df)))
# 1st Differencing
axes[1, 0].plot(df.value.diff()); axes[1, 0].set_title('1st Order Differencing')
plot_acf(df.value.diff().dropna(), ax=axes[1, 1], lags=np.arange(len(df) - 1))
plt.show()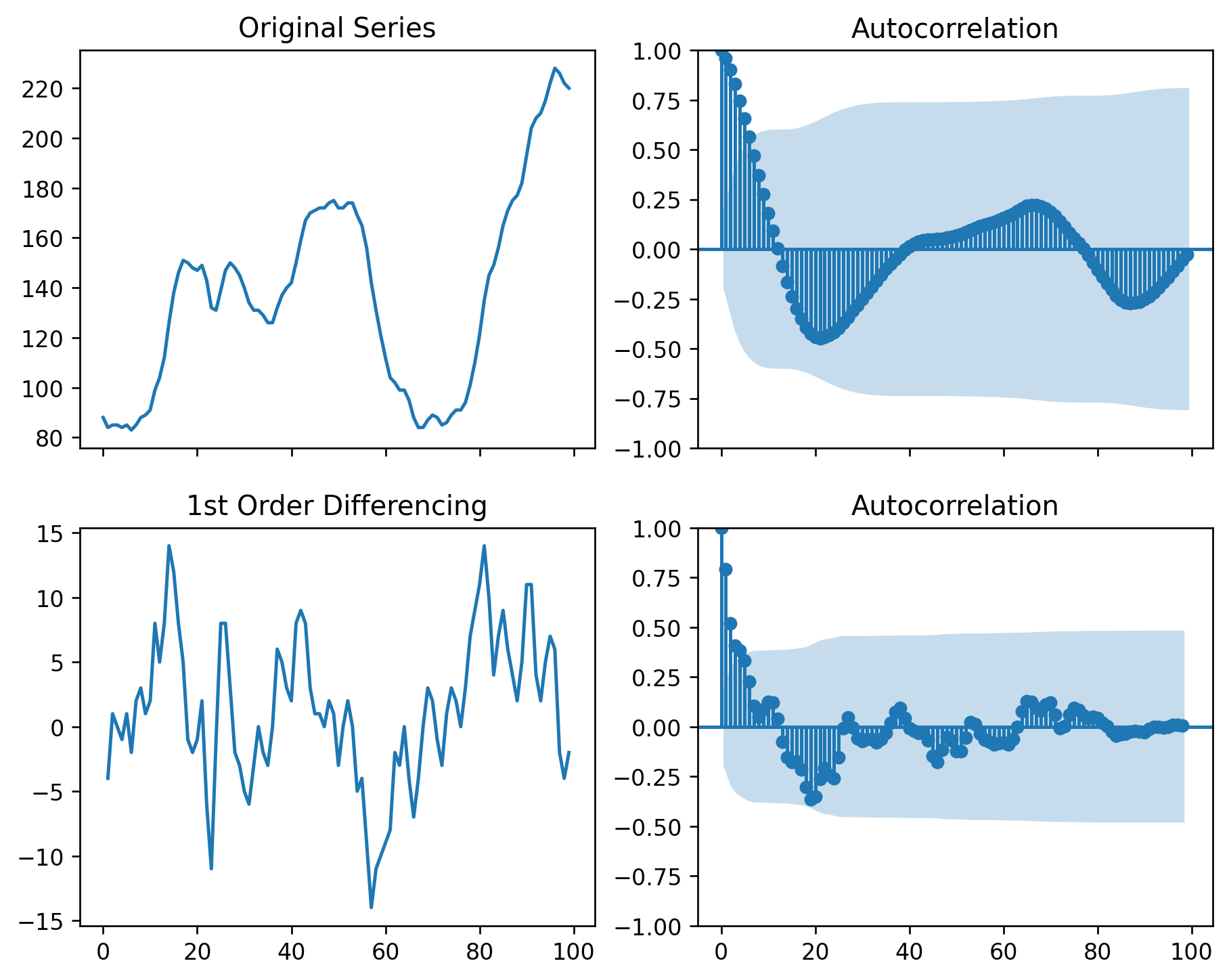
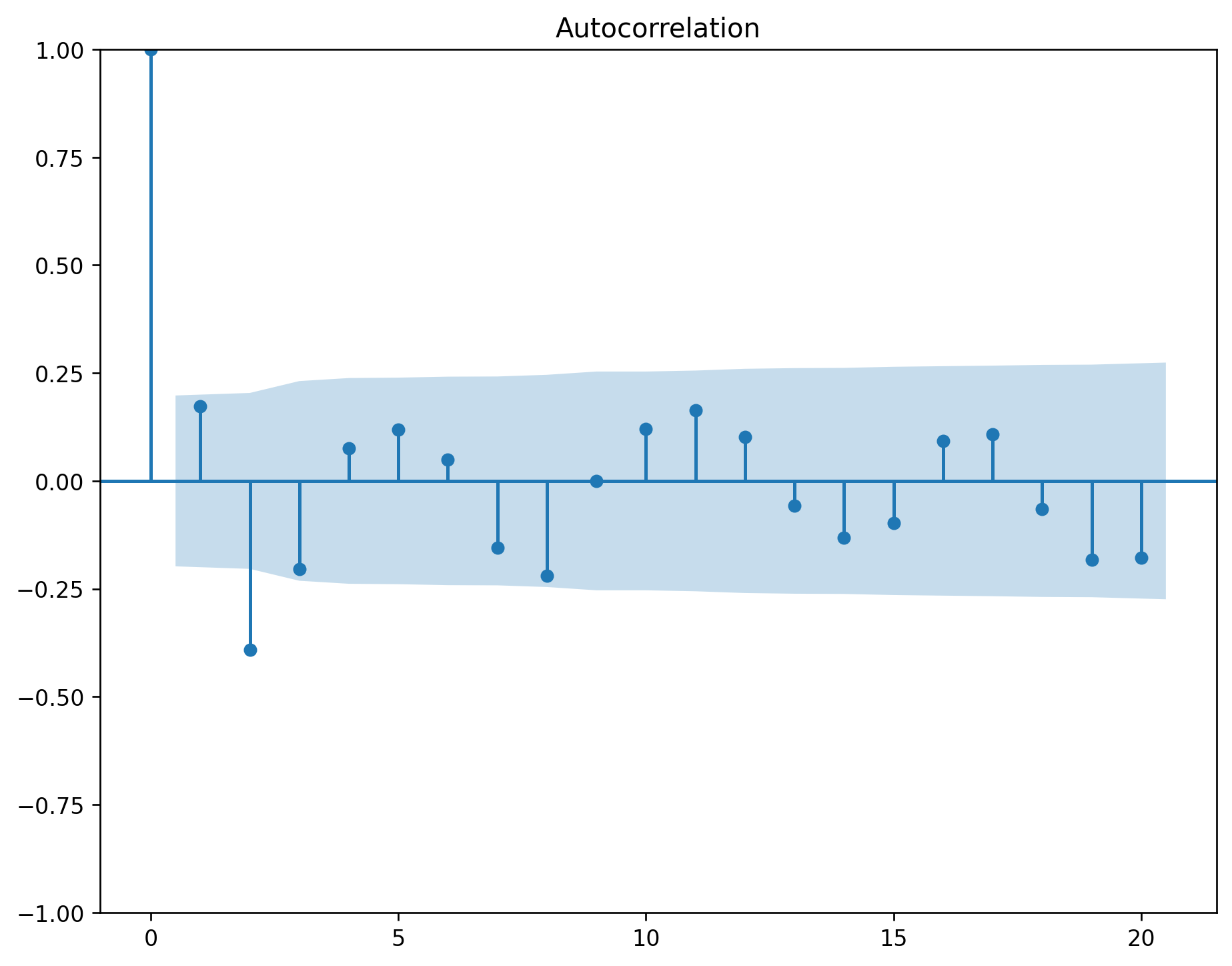
Eg:
Square root: Wt=√Yt
Logarithm: Wt=log(Yt)
This very useful.
Interpretable: Changes in a log value are relative (percent) changes on the original sclae.
airpassenger = pd.read_csv('AirPassengers.csv')
from datetime import datetime
import plotnine
from plotnine import *
airpassenger['Month']= pd.to_datetime(airpassenger['Month'])
ggplot(airpassenger, aes(x='Month', y='#Passengers'))+geom_line()<ggplot: (331734342)>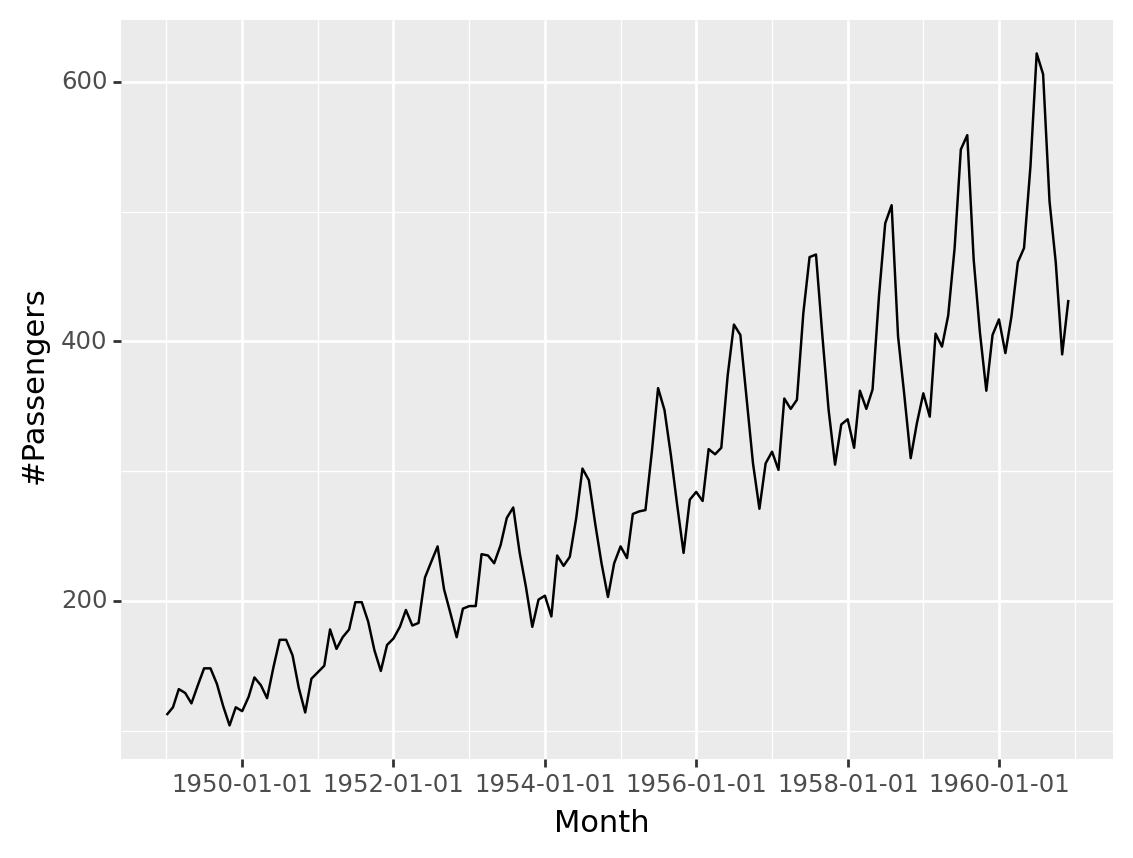
import numpy as np
airpassenger['naturallog'] = np.log(airpassenger['#Passengers'])
ggplot(airpassenger, aes(x='Month', y='naturallog'))+geom_line()<ggplot: (331805001)>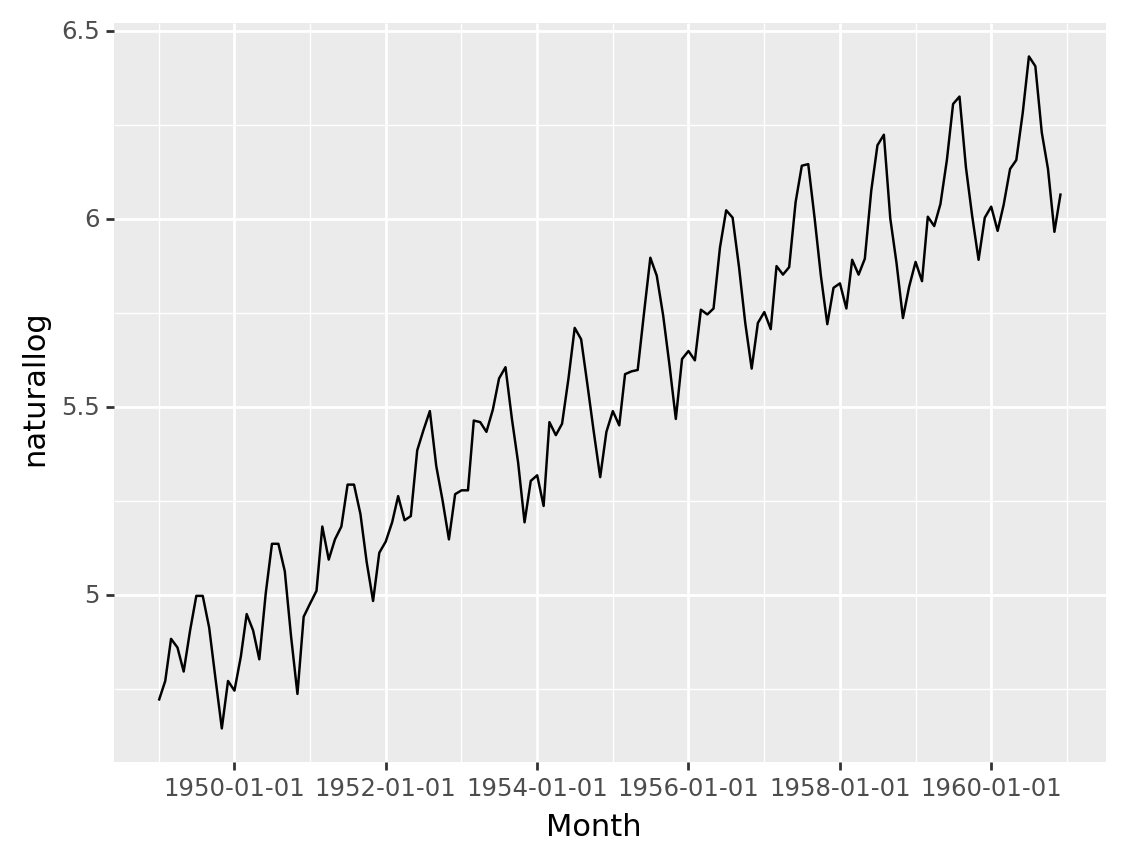
wt={log(yt),if λ=0(Yλt−1)/λ,otherwise.
Different values of λ gives you different transformations.
λ=1: No substantive transformation
λ=12: Square root plus linear transformation
λ=0: Natural logarithm
λ=−1: Inverse plus 1
Balance the seasonal fluctuations and random variation across the series.
array([ 6.82749005, 6.93282224, 7.16189151, 7.11461078, 6.98378687,
7.20826542, 7.39959794, 7.39959794, 7.22352834, 6.94993188,
6.67930112, 6.93282224, 6.88074148, 7.0663838 , 7.29843847,
7.20826542, 7.05009066, 7.41371485, 7.69297755, 7.69297755,
7.53726005, 7.17744836, 6.86312389, 7.28363955, 7.35675408,
7.42775127, 7.791663 , 7.6033268 , 7.71801394, 7.791663 ,
8.03379957, 8.03379957, 7.86322651, 7.59025293, 7.3711186 ,
7.64214252, 7.70552693, 7.81574285, 7.96693012, 7.82769741,
7.85143867, 8.23478523, 8.35415797, 8.46833738, 8.14152446,
7.94424651, 7.71801394, 7.97819691, 8.00058286, 8.00058286,
8.41186604, 8.40233549, 8.34441554, 8.47763304, 8.66568618,
8.73398286, 8.42136224, 8.16254066, 7.81574285, 8.05570781,
8.08822445, 7.90983871, 8.40233549, 8.32482145, 8.39277032,
8.66568618, 8.97573698, 8.90544371, 8.62209995, 8.34441554,
8.0774311 , 8.34441554, 8.46833738, 8.38317027, 8.69150146,
8.70857469, 8.71707079, 9.07418456, 9.41661628, 9.30252389,
9.05177744, 8.75078932, 8.42136224, 8.78409104, 8.83328615,
8.77580407, 9.08902184, 9.0592668 , 9.0964106 , 9.48162515,
9.72179099, 9.67415098, 9.35679401, 9.00640692, 8.72554012,
9.00640692, 9.07418456, 8.96801544, 9.36350433, 9.30936559,
9.35679401, 9.77445522, 10.01359054, 10.02424732, 9.66813973,
9.30252389, 8.9987716 , 9.22613489, 9.25415593, 9.0964106 ,
9.40343224, 9.30936559, 9.41003199, 9.84886109, 10.14918625,
10.21968352, 9.66813973, 9.38353935, 9.03673716, 9.23316669,
9.390186 , 9.26806127, 9.68014959, 9.61958794, 9.76283534,
10.05072014, 10.426264 , 10.4768849 , 10.00289463, 9.68613564,
9.40343224, 9.67415098, 9.74531682, 9.58881702, 9.75700771,
9.99215929, 10.05072014, 10.36531089, 10.75145254, 10.68404894,
10.23457308, 9.99215929, 9.58262264, 9.83186035])Yt=c+ϕ1Yt−1+...+ϕpYt−p+θ1ϵt−1+...+θqϵt−q+ϵt
These are stationary models.
They are only suitable for stationary series.
Differencing –> ARMA
Step 1: Differencing
Y′t=(1−B)dYt
Step 2: ARMA
Y′t=c+ϕ1Y′t−1+...+ϕpY′t−p+θ1ϵt−1+...+θqϵt−q+ϵt
Detect unusual observations in the data
Detect non-stationarity by visual inspections of plots
Stationary series:
has a constant mean value and fluctuates around the mean.
constant variance.
no pattern predictable in the long-term.
(<Figure size 1920x480 with 1 Axes>,
<AxesSubplot: ylabel='Number of airline passengers'>)Specify the forecast horizon
import numpy as np
import pandas as pd
from sktime.forecasting.base import ForecastingHorizon
fh = ForecastingHorizon(
pd.PeriodIndex(pd.date_range("1960-01", periods=12, freq="M")), is_relative=False
)
fhForecastingHorizon(['1960-01', '1960-02', '1960-03', '1960-04', '1960-05', '1960-06',
'1960-07', '1960-08', '1960-09', '1960-10', '1960-11', '1960-12'],
dtype='period[M]', is_relative=False)(<Figure size 1920x480 with 1 Axes>,
<AxesSubplot: ylabel='Number of airline passengers'>)Need transformations?
Need differencing?
(<Figure size 1920x480 with 1 Axes>,
<AxesSubplot: ylabel='Number of airline passengers'>)Identifying non-stationarity by looking at plots
Time series plot
The ACF of stationary data drops to zero relatively quickly.
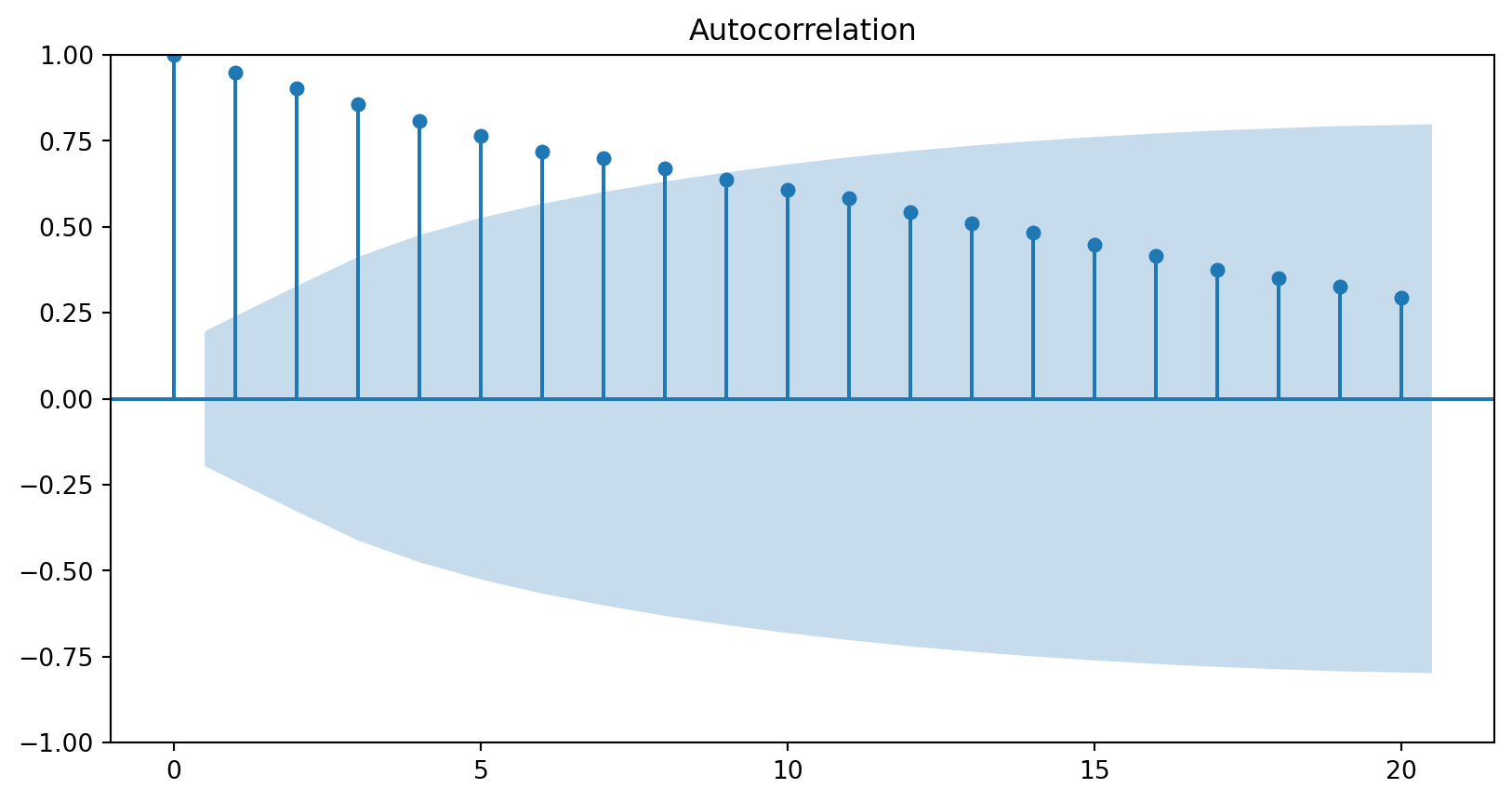
The ACF of non-stationary data decreases slowly.
For non-stationary data, the value of r1 is often large and positive.
Non seasonal first-order differencing: Y′t=Yt−Yt−1
Non seasonal second-order differencing: Y″t=Y′t−Y′t−1
Seasonal differencing: Yt−Yt−m
There are times differencing once is not enough. However, in practice,it is almost never necessary to go beyond second-order differencing.
1949-01 NaN
1949-02 NaN
1949-03 NaN
1949-04 NaN
1949-05 NaN
...
1959-08 0.101591
1959-09 0.136312
1959-10 0.125491
1959-11 0.155072
1959-12 0.183804
Freq: M, Name: Number of airline passengers, Length: 132, dtype: float641949-01 NaN
1949-02 NaN
1949-03 NaN
1949-04 NaN
1949-05 NaN
1949-06 NaN
1949-07 NaN
1949-08 NaN
1949-09 NaN
1949-10 NaN
1949-11 NaN
1949-12 NaN
1950-01 0.026433
1950-02 0.065597
1950-03 0.065958
1950-04 0.045462
1950-05 0.032523
1950-06 0.098672
1950-07 0.138586
1950-08 0.138586
Freq: M, Name: Number of airline passengers, dtype: float64Dickey and Fuller (DF) test
Augmented DF test
Phillips and Perron (PP) nonparametric test
Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test
H0: Series is level or trend stationary.
H1: Series is not stationary.
from statsmodels.tsa.stattools import kpss
def kpss_test(series, **kw):
statistic, p_value, n_lags, critical_values = kpss(series, **kw)
# Format Output
print(f'KPSS Statistic: {statistic}')
print(f'p-value: {p_value}')
print(f'num lags: {n_lags}')
print('Critial Values:')
for key, value in critical_values.items():
print(f' {key} : {value}')
print(f'Result: The series is {"not " if p_value < 0.05 else ""}stationary')
kpss_test(y_train.naturallog)KPSS Statistic: 1.9204939010623039
p-value: 0.01
num lags: 6
Critial Values:
10% : 0.347
5% : 0.463
2.5% : 0.574
1% : 0.739
Result: The series is not stationaryKPSS Statistic: 0.29885781439314946
p-value: 0.1
num lags: 5
Critial Values:
10% : 0.347
5% : 0.463
2.5% : 0.574
1% : 0.739
Result: The series is stationaryKPSS test may not necessarily reject the null hypothesis (that the series is level or trend stationary) even if a series is steadily increasing or decreasing.
The word ‘deterministic’ implies the slope of the trend in the series does not change permanently. That is, even if the series goes through a shock, it tends to regain its original path.
source: https://www.machinelearningplus.com/time-series/kpss-test-for-stationarity/
By default, it tests for stationarity around a ‘mean’ only.
To turn ON the stationarity testing around a trend, you need to explicitly pass the regression=‘ct’ parameter to the kpss
KPSS Statistic: 0.0760056301424143
p-value: 0.1
num lags: 5
Critial Values:
10% : 0.119
5% : 0.146
2.5% : 0.176
1% : 0.216
Result: The series is stationaryfrom statsmodels.tsa.stattools import adfuller
def adf_test(series):
result = adfuller(series, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
print('Critial Values:')
print(f' {key}, {value}')
series = df.loc[:, 'value'].valuesH0: Series is not stationary
H1: Series is stationary
ADF Statistic: -1.3176112021439967
p-value: 0.6210771494355872
Critial Values:
1%, -3.4870216863700767
Critial Values:
5%, -2.8863625166643136
Critial Values:
10%, -2.580009026141913ADF Statistic: -2.5844902417566793
p-value: 0.09624537566648711
Critial Values:
1%, -3.492995948509562
Critial Values:
5%, -2.888954648057252
Critial Values:
10%, -2.58139291903223If a series is stationary according to the KPSS test by setting regression=‘ct’ and is not stationary according to the ADF test, it means the series is stationary around a deterministic trend.
Further reading:
Kwiatkowski, D.; Phillips, P. C. B.; Schmidt, P.; Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54 (1-3): 159-178.
ACF dies out in an exponential or damped sine-wave manner.
there is a significant spike at lag p in PACF, but none beyond p.
ACF has all zero spikes beyond the qth spike.
PACF dies out in an exponential or damped sine-wave manner.
a spike at lag 12 in the ACF but no other significant spikes.
The PACF will show exponential decay in the seasonal lags 12, 24, 36, . . . .
exponential decay in the seasonal lags of the ACF.
a single significant spike at lag 12 in the PACF.
d=1 and D=1 (from step 4)
Significant spike at lag 1 in ACF suggests non-seasonal MA(1) component.
Significant spike at lag 12 in ACF suggests seasonal MA(1) component.
Initial candidate model: ARIMA(0,1,1)(0,1,1)12.
By analogous logic applied to the PACF, we could also have started with ARIMA(1,1,0)(1,1,0)12.
Initial model:
ARIMA(0,1,1)(0,1,1)12
ARIMA(1,1,0)(1,1,0)12
Try some variations of the initial model:
ARIMA(0,1,1)(1,1,1)12
ARIMA(1,1,1)(1,1,0)12
ARIMA(1,1,1)(1,1,1)12
Try some variations
Both the ACF and PACF show significant spikes at lag 3, and almost significant spikes at lag 3, indicating that some additional non-seasonal terms need to be included in the model.
ARIMA(3,1,1)(1,1,1)12
ARIMA(1,1,3)(1,1,1)12
ARIMA(3,1,3)(1,1,1)12
from sktime.forecasting.arima import ARIMA
forecaster1 = ARIMA(
order=(1, 1, 0),
seasonal_order=(1, 1, 0, 12),
suppress_warnings=True)
forecaster1.fit(y_train.naturallog) ARIMA(order=(1, 1, 0), seasonal_order=(1, 1, 0, 12), suppress_warnings=True)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
ARIMA(order=(1, 1, 0), seasonal_order=(1, 1, 0, 12), suppress_warnings=True)
fhtrain = ForecastingHorizon(
pd.PeriodIndex(pd.period_range(start='1949-01', end='1959-12', freq='M')), is_relative=False
)
fhtrainForecastingHorizon(['1949-01', '1949-02', '1949-03', '1949-04', '1949-05', '1949-06',
'1949-07', '1949-08', '1949-09', '1949-10',
...
'1959-03', '1959-04', '1959-05', '1959-06', '1959-07', '1959-08',
'1959-09', '1959-10', '1959-11', '1959-12'],
dtype='period[M]', length=132, is_relative=False)Your turn: remove the outlier and draw the histogram
H0: Residuals are not serially correlated.
H1: Residuals are serially correlated.
| lb_stat | lb_pvalue | |
|---|---|---|
| 20 | 3.984776 | 0.999955 |
(<Figure size 1920x480 with 1 Axes>,
<AxesSubplot: ylabel='Number of airline passengers'>)Fit other variants of ARIMA models and identify the best ARIMA model for the series.
Plot the data.
If necessary, transform the data (using a Box-Cox transformation) to stabilise the variance.
If the data are non-stationary, take first differences of the data until the data are stationary.
Examine the ACF/PACF to identify a suitable model.
Try your chosen model(s), and use the AICc to search for a better model.
Check the residuals from your chosen model by plotting the ACF of the residuals, and doing a portmanteau test of the residuals. If they do not look like white noise, try a modified model.
Once the residuals look like white noise, calculate forecasts.
Source: Forecasting: Principles and Practice, Rob J Hyndman and George Athanasopoulos