from sktime import *
from sktime.datasets import load_airline
from sktime.utils.plotting import plot_series
y = load_airline()
plot_series(y)(<Figure size 1536x384 with 1 Axes>,
<AxesSubplot: ylabel='Number of airline passengers'>)
Week 5A: AutoARIMA
Modelling steps
Plot the data.
If necessary, transform the data (using a Box-Cox transformation) to stabilise the variance.
3. If the data are non-stationary, take first differences of the data until the data are stationary.
4. Examine the ACF/PACF to identify a suitable model.
5. Try your chosen model(s), and use the AICc to search for a better model.
Modelling steps (cont.)
Check the residuals from your chosen model by plotting the ACF of the residuals, and doing a portmanteau test of the residuals. If they do not look like white noise, try a modified model.
Once the residuals look like white noise, calculate forecasts.
Modelling steps: AutoARIMA
Plot the data.
If necessary, transform the data (using a Box-Cox transformation) to stabilise the variance.
Use AutoARIMA to select a model.
Check the residuals from your chosen model by plotting the ACF of the residuals, and doing a portmanteau test of the residuals. If they do not look like white noise, try a modified model.
Once the residuals look like white noise, calculate forecasts.
Modeling with Python
Your turn
Take other important visualizations
Define forecast horizon
import numpy as np
import pandas as pd
from sktime.forecasting.base import ForecastingHorizon
fh = ForecastingHorizon(
pd.PeriodIndex(pd.date_range("1960-01", periods=12, freq="M")), is_relative=False
)
fhForecastingHorizon(['1960-01', '1960-02', '1960-03', '1960-04', '1960-05', '1960-06',
'1960-07', '1960-08', '1960-09', '1960-10', '1960-11', '1960-12'],
dtype='period[M]', is_relative=False)Split data into training and test
Define forecaster with sktime
from sktime.forecasting.statsforecast import StatsForecastAutoARIMA
import numpy as np
forecaster = StatsForecastAutoARIMA(
sp=12, max_p=2, max_q=2
)
y_train.naturallog = np.log(y_train)
forecaster.fit(y_train.naturallog)StatsForecastAutoARIMA(max_p=2, max_q=2, sp=12)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
StatsForecastAutoARIMA(max_p=2, max_q=2, sp=12)
sp: Number of observations per unit of time.
Help: https://www.sktime.org/en/stable/api_reference/auto_generated/sktime.forecasting.statsforecast.StatsForecastAutoARIMA.html
Your turn
Preferm residual analysis
Obtain predictions for the training period
Prediction intervals
| Coverage | ||
|---|---|---|
| 0.9 | ||
| lower | upper | |
| 1960-01 | 5.978520 | 6.099244 |
| 1960-02 | 5.916820 | 6.062361 |
| 1960-03 | 6.062679 | 6.229384 |
| 1960-04 | 6.026940 | 6.212408 |
| 1960-05 | 6.058205 | 6.260705 |
| 1960-06 | 6.195598 | 6.413804 |
| 1960-07 | 6.316247 | 6.549103 |
| 1960-08 | 6.321487 | 6.568124 |
| 1960-09 | 6.136959 | 6.396648 |
| 1960-10 | 6.000121 | 6.272235 |
| 1960-11 | 5.865717 | 6.149713 |
| 1960-12 | 5.966786 | 6.262187 |
Plotting values
y_test.naturallog = np.log(y_test)
from sktime.utils import plotting
# also requires predictions
y_pred = forecaster.predict()
fig, ax = plotting.plot_series(y_train.naturallog, y_pred, labels=["y", "y_pred"])
ax.fill_between(
ax.get_lines()[-1].get_xdata(),
y_pred_ints["Coverage"][coverage]["lower"],
y_pred_ints["Coverage"][coverage]["upper"],
alpha=0.2,
color=ax.get_lines()[-1].get_c(),
label=f"{coverage}% prediction intervals",
)
ax.legend();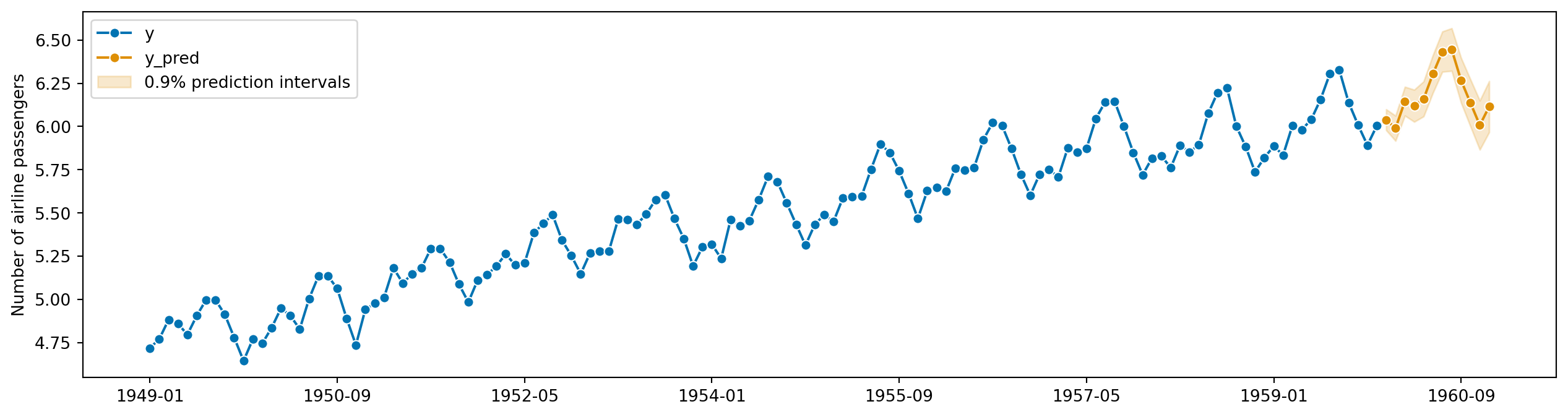
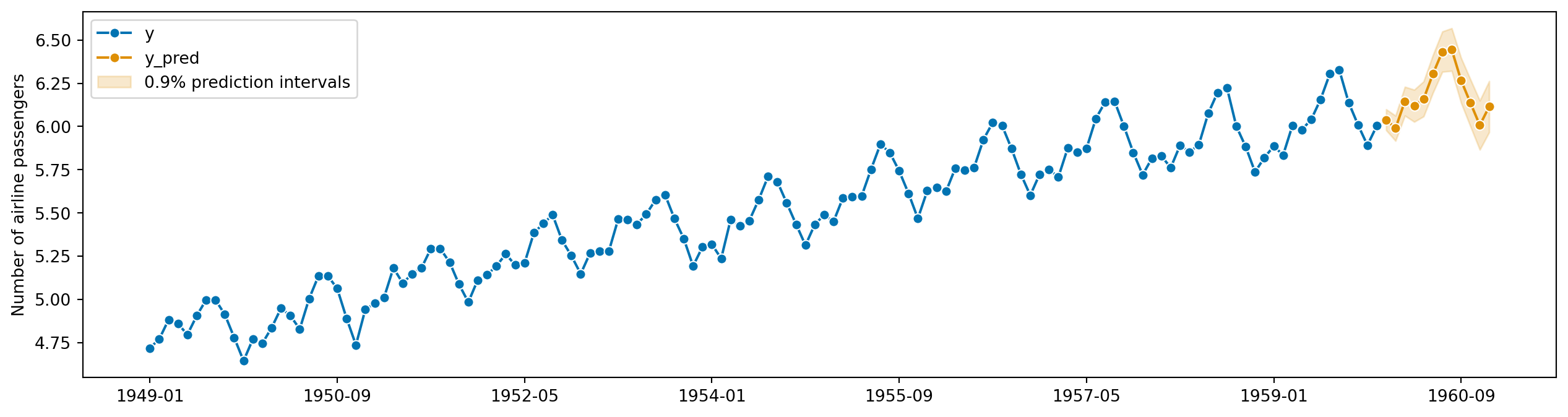
What is happening under the hood of AutoARIMA?
Step 1: Select the number of differences d and D via unit root tests and strength of seasonality measure.
Step 2: Try four possible models to start with:
ARIMA(2,d,2) if m=1 and ARIMA(2,d,2)(1,D,1)m if m>1.
ARIMA(0,d,0) if m=1 and ARIMA(0,d,0)(0,D,0)m if m>1.
ARIMA(1,d,0) if m=1 and ARIMA(1,d,0)(1,D,0)m if m>1.
ARIMA(0,d,1) if m=1 and ARIMA(0,d,1)(0,D,1)m if m>1.
Step 3: Select the model with the smallest AICc from step 2. This becomes the current model.
Step 4: Consider up to 13 variations on the current model:
Vary one of p,q,P and Q from the current model by ±1.
p,q both vary from the current model by ±1.
P,Q both vary from the current model by ±1.
Include or exclude the constant term from the current model. Repeat step 4 until no lower AICc can be found.
Week 5A: AutoARIMA